Modelling audio trilateration

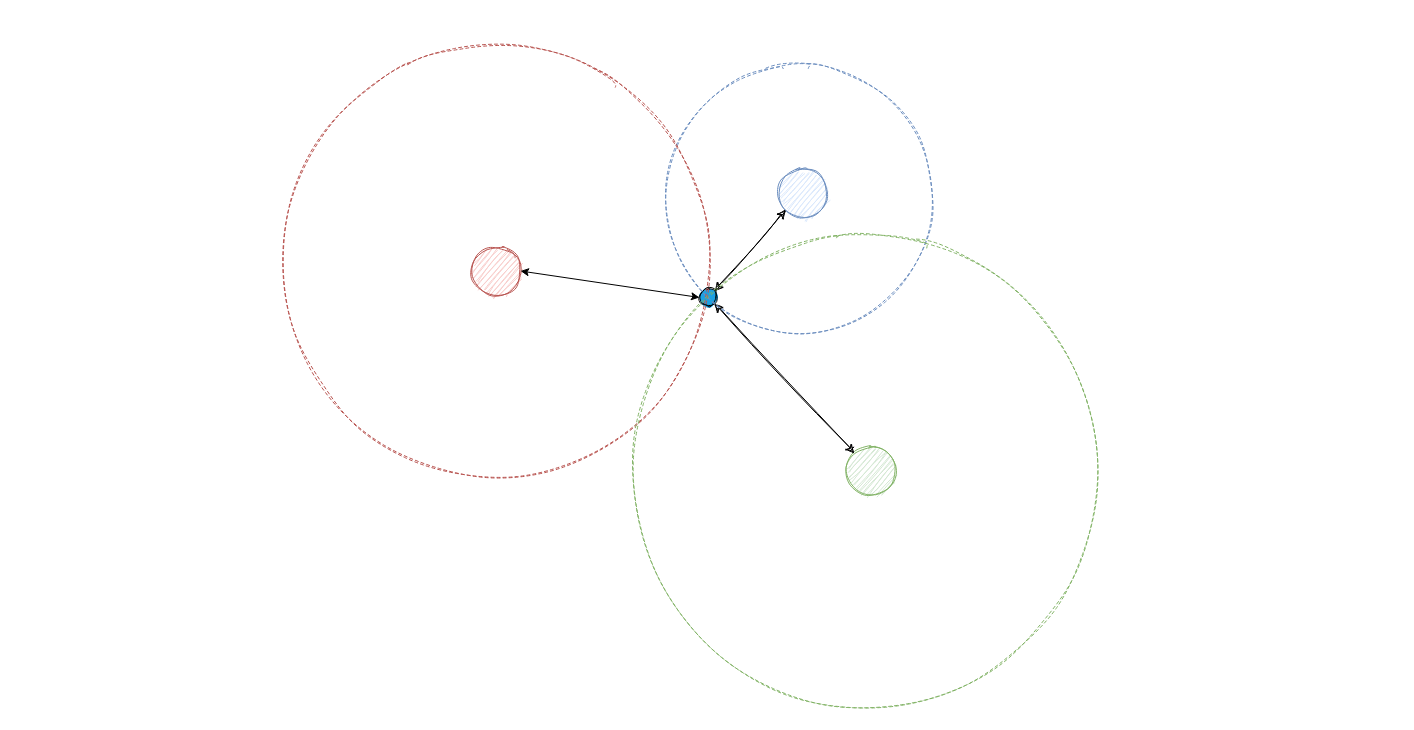
Trilateration is the act of finding a location given a set of distances from known locations. It is a little different from triangulation where you know the angles from known locations.

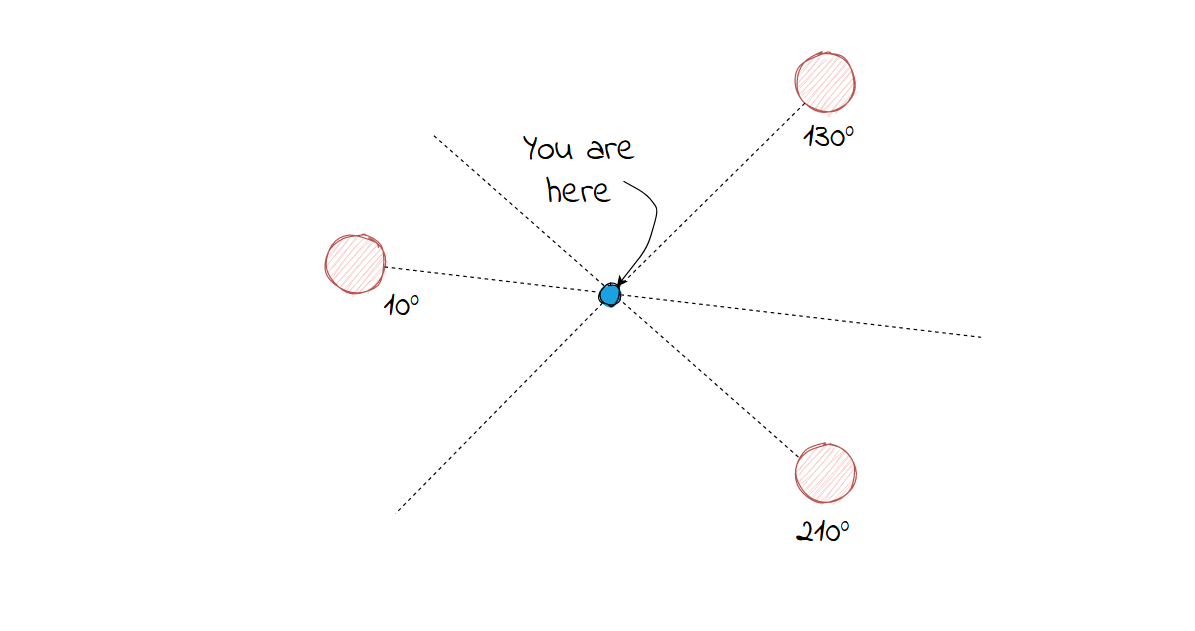
With triangulation, you measure the angle and find the intersections.

With trilateration you find the distance from the center to each of the shaded circles to determine the location of the origin.

Now to picture the problem, since audio signals radiate out from a single point, and you don't know the direction, the only info is the time which each node detects the sound.

The dotted rings indicate where each of the shaded nodes would hear the sound emitted by the object in the center.

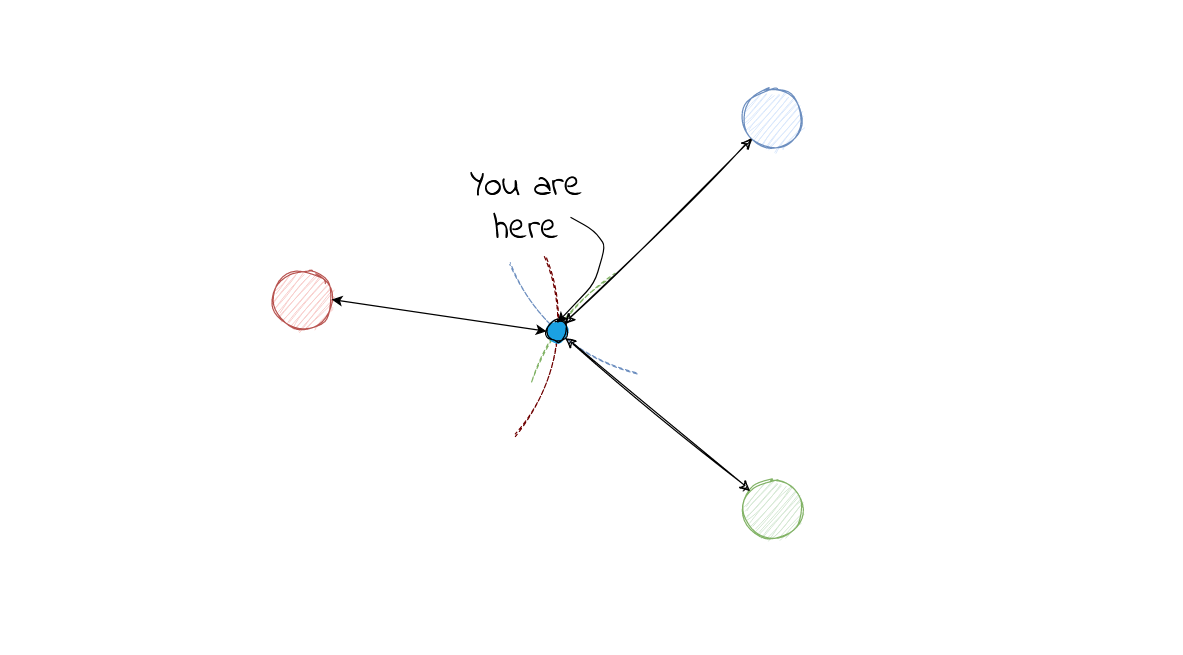
In terms of the an observer timing when each node would detect the sound, the information returned would be in the diagram below. At the start of listening, node A will hear it first, followed by node B and then node C.

Since sound travels at a fixed speed, by knowing the time that each node hears the sound, we know roughly how far the origin of the sound is from the nodes. However, note that we don't have the orientation at this point of them, but we know the position of these nodes (since we put them there)

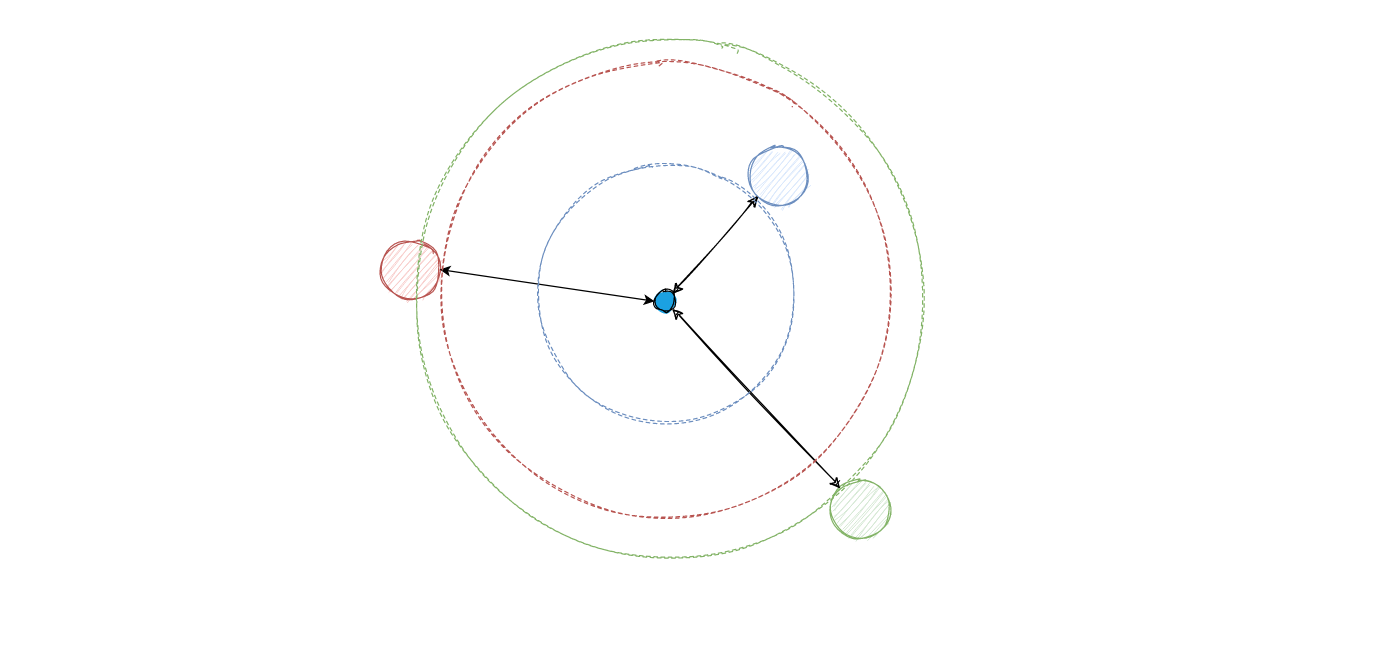
If you flip the perspective and consider it from the point of view from the nodes (i.e. replay the signal backwards), the graph above is actually equivalent to each node emitting a signal at different points in time. To each of these nodes, the ring represents the possibility space where the origin of sound could be (we know the distance but not the origin).

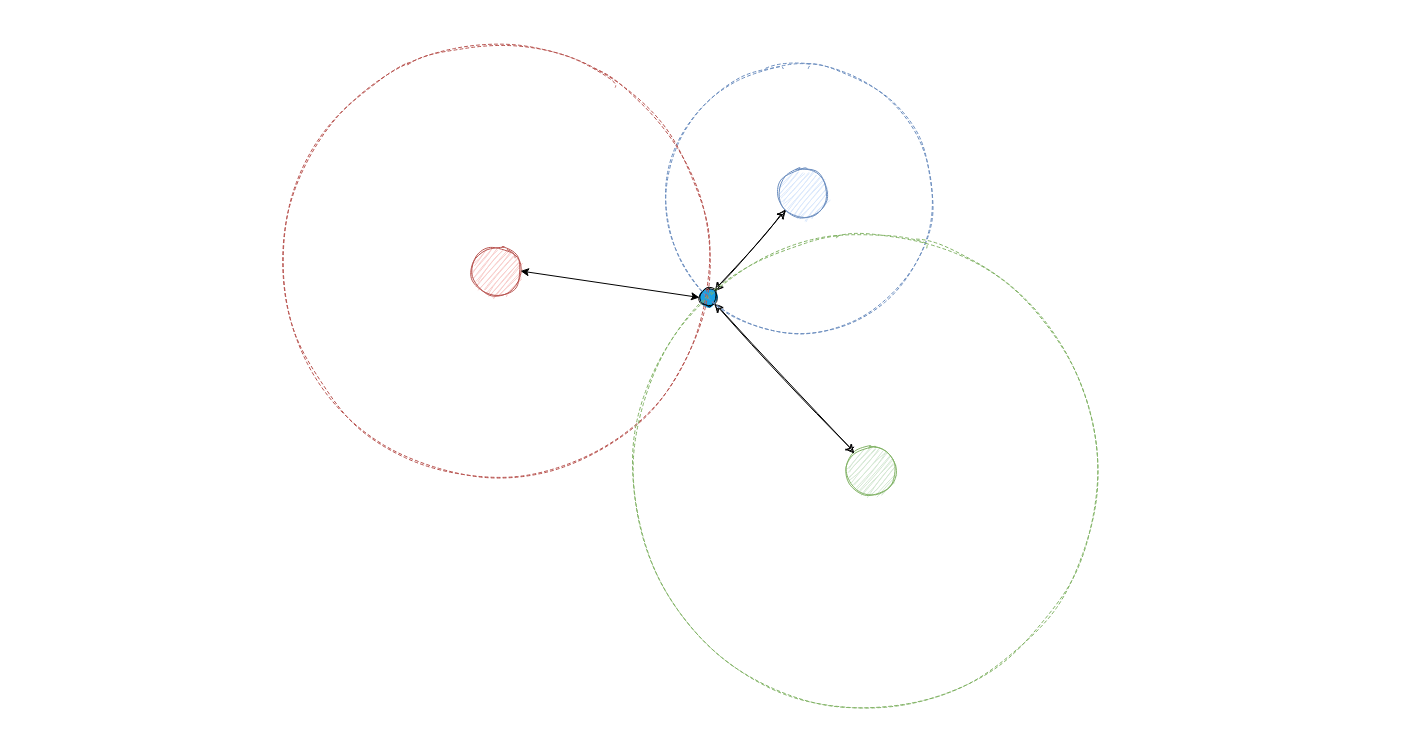
The point where all these signals intersect is then the origin. There is no other possibility where these three circles intersect. Given the location of these nodes, we can simply solve the system of equation of which these three circles intersect, with the radius being given by the time which each signal is received by the node multiplied by the speed:

\[(x - x_{\text{node}})^2 + (y -  y_{\text{node}})^2 = t_{\text{node}} \times v_{\text{sound}}\]

This value would be considering a perfect system. If there is some level of uncertainty when it comes to detecting the time of the sound, then there wouldn't be a point which three circles intersect but an area.

Consider a listening node detecting a sound at time $t$. The range of possible locations that this sound could have originated from would be a ring around this node. If it were to detect a sound at time $t + \delta t$, then this would be represented as another concentric circle wider than the first. Now given that $\delta t$ is the jitter that a node detects the sound,

\[ t < t_{\text{actual} < t+\delta t}\]

This means that the location of the sound's origin can lie anywhere between these two concetric circles.

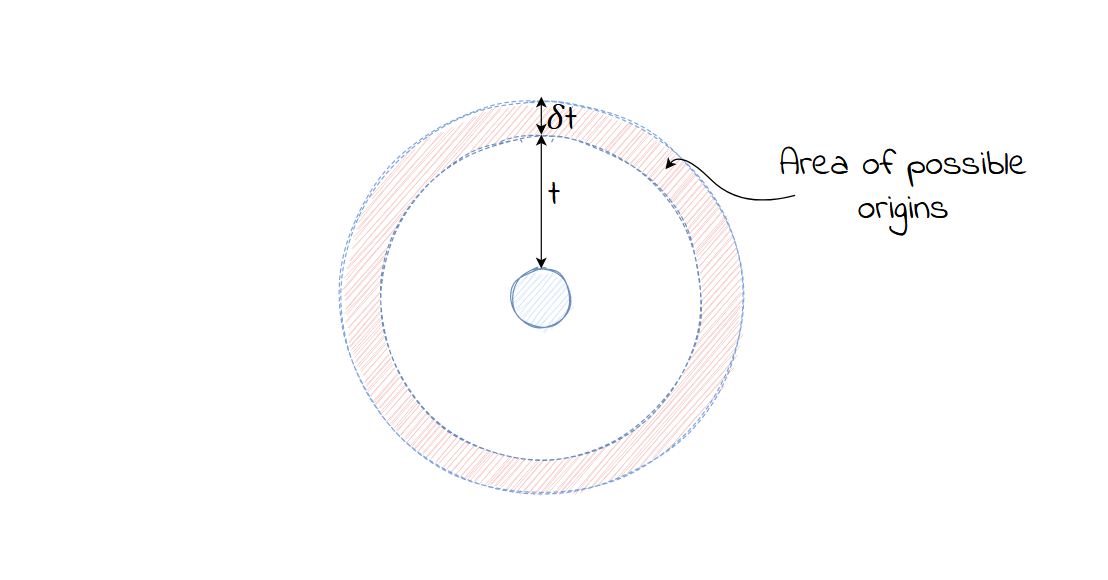
Instead of a nice geometrical solution by drawing intersecting circles and calculating the intersect, it is harder now as the location of possible origins is represented as a donut centered at each node, and the area which they intersect is not a regular one.

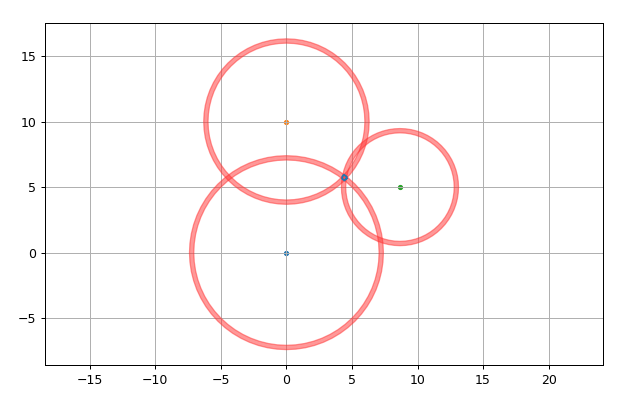
Therefore, instead of an analytical solution, I resorted to using a numerical one. Since Python has some great GIS libraries, I used the shapes that you can generate with these libraries to help generate a search area. The general process follows:

1. Draw two circles and subtract the smaller circle from the larger one to determine the band of possible origins. I did this is shapely in Python.
2. Repeat 1. for each node.
3. With these three bands, obtain the shape by performing an intersect operation on each of the bands, and then calculate the area of the resulting shape.
4. Plot it in in Matplotlib to determine graphically if the answer made sense (it did), and to provide a visualization of how it would look like.

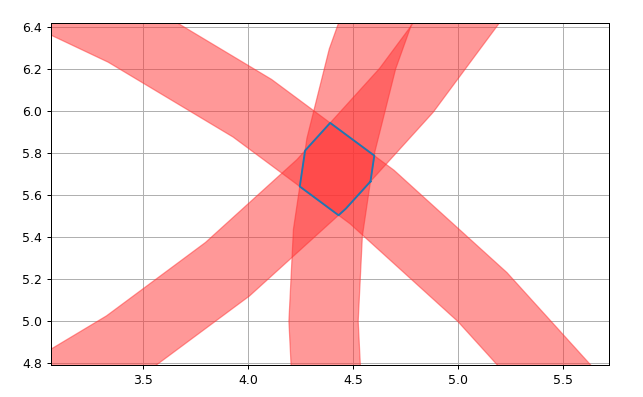
As seen, the shape is a little irregular, so it is not very practical to describe as an empirical solution.

I also added the option to manually click the diagram to generate the origin, and to visualize what the search area would look like. It works even for origins outside of the listening nodes!

This was a simple exploration of how audio trilateration with some error can be modelled in Python, I thought it was fun to build, and hopefully the method of how I built it will be useful to someone out there!