PID Autotuning: A practical example
Tuning PID the easy way.
PID can be a real pain to tune. This is especially true if you are dealing with inherently unstable systems like a quadcopter. Ask anyone who has tuned a quadcopter manually. It is a very gruelling process that tests your patience and sanity. I remember seeing an improvement in performance as we tuned the code, only to discover that we were compiling the wrong piece of code. It is even worse if you have no idea where the target value should be.
Tuning PID is also a big hassle, so I decided to write a Nelder-Mead algorithm that searches over the possible combinations of coefficients that minimised a criteria that I specified.
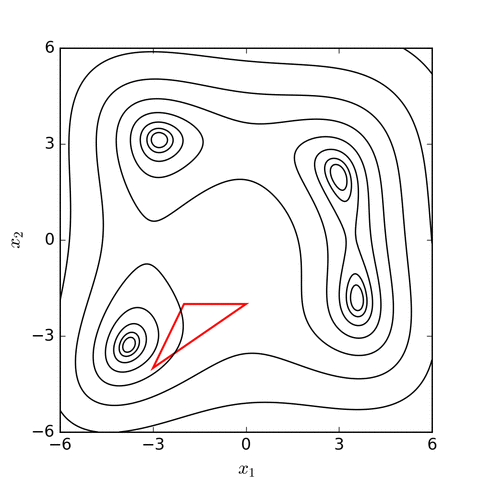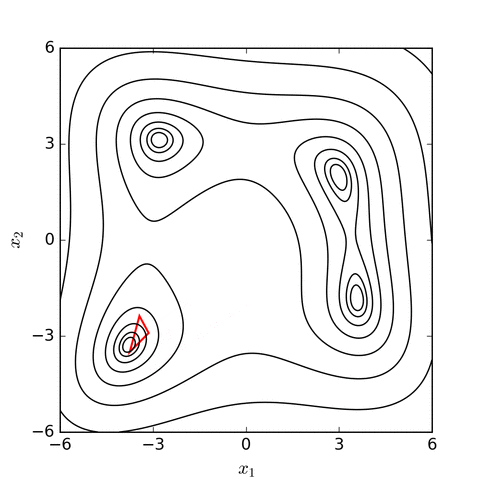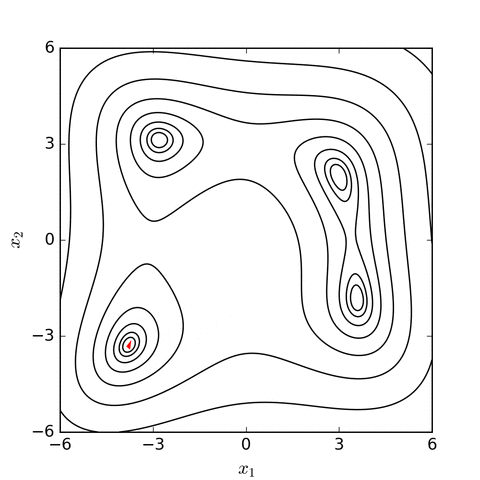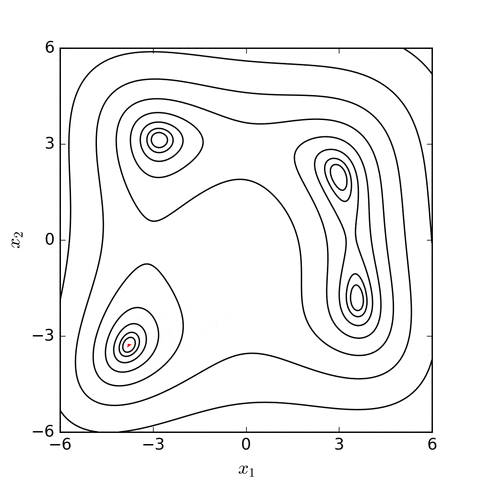
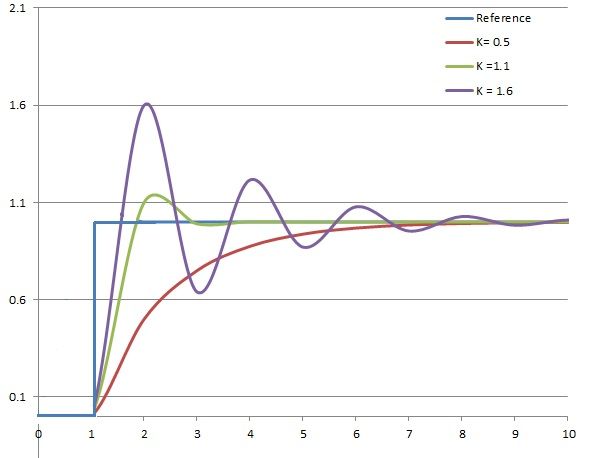
I decided to specify the sum of the absolute difference between the desired value and the current value over a limited span of time as the "score" for a particular set of PID values. This approximates the behaviour that I wanted from my controller: a short rise time and minimal oscillations. Initially, I just measured the time it took to get to a certain value, but the result was that the coefficients that I obtained had some oscillations in them. Fixing that led to better values that stablised quickly.
Another modification that I made was to use 4 points for my search because I was doing a search in 3-space for 3 different values, and the Nelder-Mead search specifies that the number of verticies should be n+1 more than the number of dimensions. This yielded much better results than the 3 point search I was attempting in an earlier experimentation.
Since the Nelder-Mead method was implemented, there are no constraints on the values, so it could be negative. Therefore I also included additional code that checks if any coefficient is negative. If they are, the score for that set is the worst possible score. This maintains the algorithm by changing the reward function, ensuring the least possible deviation from the actual algorithm.
The autotuning process paid off handsomely. Previously using manually tuned values I was able to get an error of up to 20 counts because of a deadzone. However, the autotuning mechanism managed to get an error of 2 counts in position control. It also turned out that the search yielded a result that had a proportional controller that was 3 times bigger than what I had used previously.
Potential Issues
One problem with the Nelder Mead search is that the initial values are very important. Some knowledge of the search space is required, otherwise it could get trapped in a local maximum/pleateu.
Code
The code that I have written is in C and implemented as part of a generic series of code that I have found to be useful in microcontroller programming, especially for control. The code can be found in the file gen_algo.c at: https://github.com/benlhy/TIVA-Motion-Module
References
[1] By Nicoguaro - Own work, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=51597577
[2] Header image, By TimmmyK - Own work, CC0, https://commons.wikimedia.org/w/index.php?curid=36662015
